辅导孩子作业是令不少家长头疼的问题。最近,一道数学题又难住了不少家长。“0.999…和1到底谁大?”不少家长认为:“当然是1大。”直到一名家长找到AI求证讲题后,得到的结果竟然是“0.999…=1”。家长们纷纷感慨“原本还在生气这么简单的题目孩子都不会,下一秒发现小丑竟是自己!”此事引发众多家长和网友参与讨论,一度登上了新浪微博热搜榜。
针对这一网络热搜,现代快报记者采访了常州市博爱教育集团数学老师张丽,她表示,这道题目其实蕴含了数学的极限思想。学校曾在数学拓展课程中,让孩子们通过各种方法思辨究竟谁大。相比于最终的结果,张丽认为学生们对于数学问题的探究兴趣和思考方法更加重要。
据白鹿视频消息,近日,一道简单的小学数学题难住了众家长。“刚刚让孩子给我整蒙了,他问我0.999…和1谁更大?我就寻思,这题还用问吗?这难道不是1更大?”网名为“然然妈”的家长将这一疑惑发在了家长群里。
不少家长纷纷加入讨论:“肯定是1啊!”“难道不是1?”“0.999…是无限循环小数,只是接近1,但应该永远小于1才对。”……
群里不少家长都认为答案是“1大”,也有个别家长不确定地表示“这个我咋记得是一样大”。
有家长想到了求助AI,最后得到的结果竟然是“0.999…=1”。这个结果让家长们大跌眼镜。“然然妈”表示:“我这刚苦口婆心跟孩子讲完为啥1更大,合着是我错了?”
此事被发至网络后,也引发了众多网友的讨论,一度登上了微博热搜榜。一些网友在得知答案后,表示“突然发现自己这么多年学好像白上了”。有网友总结此事的经验教训:“看来在辅导孩子时,不能光靠感觉,要多一分钻研,多一分理性思考。”
昨天中午,现代快报记者联系上常州市博爱教育集团教导处主任张丽老师,她从事数学教学工作已近20年。张丽老师坦言,这道数学题中所蕴含的极限思想更值得大家深究。

△博爱小学“博爱讲坛”曾针对此问题进行拓展
对于“0.999…和1哪个大?”很多人会有这样的误区:无限循环小数的位数是无限的,但永远达不到1,永远小于1。张丽表示,其实这种片面的观念仍旧是因为用有限的观点来看待无限而造成的。如果借助数学上的极限方法来解决,其实0.999…是1的另一种写法或者是另一种表达方式。

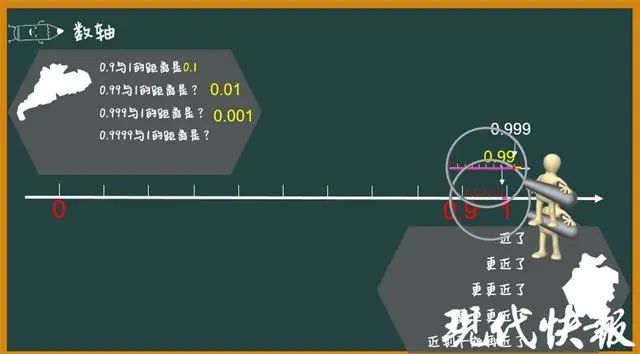
张丽介绍,早在2018年,博爱小学每周一次的“博爱讲坛”上,学生就针对这个问题开展过主题为“循环之美”的拓展活动。如何证明“0.999…=1”,孩子们产生了很多的方法,例如:1÷9=0.1111无限循环;2÷9=0.2222无限循环;3÷9=0.3333无限循环;那么以此类推,9÷9=0.9999无限循环,而9÷9=1,所以它俩一样大;又比如:通过数形结合法,把长度为1的线段无限细分并取走0.9+0.09+0.009+……,如此无限取下去,依据极限思想,可得0.999…=1。
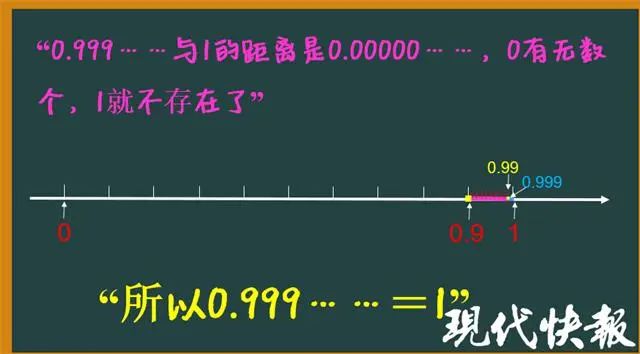
△博爱小学“循环之美”数学拓展课程课件
张老师说其实数学的这种极限思想在我们的生活中和数学学习中处处可见。比如庄子就曾在《庄子·天下篇》中说过:“一尺之锤,日取其半,万世不竭。”意思就是一尺长的木棍,一天截一半,永远也截不完。换成数学来代表就是:1/2、1/4、1/8……1/2的n次方。
再比如刘徽为计算圆面积和圆周率,曾经创立了“割圆术”,从圆内接正六边形计算,边数逐步加倍,相继算出正12边形、正24边形等,则圆内接正多边形逐渐逼近圆,其周长的极限即为圆周长,面积的极限即为圆面积。“割圆术就包含了极限的概念。”
从汉语拼音“O”究竟怎么读到0.999…和1到底谁大,家长们在辅导孩子作业过程中,已经发生过不少自我感觉和正确答案相违背的事例。
一名小学一年级学生家长告诉记者,她在辅导孩子作业时,经常会在生字笔画上蒙圈。“比如像四会字‘万’,我们平常写,第二笔是撇,但现在孩子们学的知识体系里,正确的笔顺第二笔应该是横折钩,‘方’字也是如此。一开始我以为小孩写错了,最后发现我自己的才是错的,有点蒙。”
另一名小学二年级家长向记者表示,今年孩子刚刚学习了乘法和除法运算,在除法算式里,被除数是指除号前面的数字,而除数是除号后面的数字。“我们小时候估计没有太强调这个,我想当然以为被除数是被除的,所以以为是除号后面的,看了数学书上才发现原来被除数是表示被另一个数所除的数,所以是除号前面那个数字。”
不少家长感慨:“这年头辅导孩子作业,不仅是个体力活,还是个脑力活,更是个技术活!”
对此,张丽表示,让学生知道0.999…=1并不是教学的目的,“让孩子发现0.999…为什么等于1?用什么方法去证实?这才是教学的目的,即过程大于结果。在新课标教学中,激发学生的学习兴趣,注重学生的学习方法和学习能力才是我们重点关注的内容。”
她也建议家长们,在辅导孩子作业过程中,更应该关注孩子在校的学习习惯到了家里能否保持。当辅导时遇到疑问,应该及时咨询任课老师,说不定孩子的疑问就会成为教学的一个素材。“当时0.999…=1这个知识点就是从孩子们的疑问开始的,最终拿到了课堂进行拓展讨论。”
